Pavlov

Extending their simulations (Nowak and Sigmund 1993a) to more complex strategies and taking not only the opponent's last move but also one's own into account, the decision rule is given by a four-dimensional vector (p₁, p₂, p₃, p₄) for cooperating after R, S, T and P. [e.g. TFT: (1, 0, 1, 0); Grim: (1, 0, 0, 0) after a single D of the opponent never revert to C again].
Each of the 40 simulations was started with the random strategy (0.5, 0.5, 0.5, 0.5) and at every 100th generation (on average) a small amount of one of 10⁵ randomly chosen different mutant strategies was introduced. Mutations were limited to p₁-p₄; all other parameters (i.e. w, R, S, T, P, etc.) were fixed. The frequencies evolved according to the rules described above. Fig. 4 shows a scenario that is similar to that of the Punctuated equilibrium (Eldredge and Gould 1972): rapid shifts in the beginning, followed by an increase of defective strategies, replaced by a short phase of stable TFT-like dominance and finally substituted by GTFT or, in more than 80%, of the simulations, by a new strategy. The newcomer was close to (1, 0, 0, 1): cooperate after R and P, defect after S and T - in other words, stay with the previous decision after scoring the higher payoffs R and T and switch after S and P.

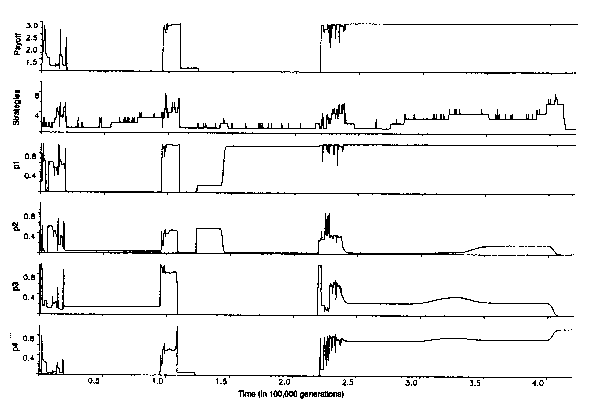
Fig. 4. An evolutionary simulation of strategies involved in the IPD. The simulation was opened with the random strategy (0.5, 0.5, 0.5, 0.5). In each generation there is a 0.01 probability of mutation (i.e. randomising p₁ and p₂). The relative frequencies were distributed according to the payoffs in the previous generation. Strategies with frequencies below 0.001 were discarded. Here, violent initial shifts are followed by the dominance of an ALLD-like mutant. At t = 92 000 a TFT-like strategy invades and gets overrun by GTFT. As more forgiving strategies drift into the cooperative society, defective strategies are able to invade and defection, dominated by Grim (0.999, 0.001, 0.001, 0.001) is the rule. Again TFT invades and is superseded, this time by the Pavlov-like (0.999, 0.001, 0.007, 0.946). This persists until t = 107 (not shown). The figure shows the average population payoff. the total number of strategies and the population averages of p1 through p4. See text for more details. From: Nowak, M. A. and Sigmund, K. 1993. A strategy of win-stay lose-shift that outperforms tit-for-tat in the prisoner's dilemma game. Nature 364: 57.

Because of its reflexive nature, Nowak and Sigmund dubbed it "Pavlov", but corresponding rather to operant than to classical conditioning, it should reasonably have been called "Skinner", for example. Anyway, Pavlov's advantage over TFT is based on two important features: it can correct occasional mistakes and prevents invasion of strict cooperators by exploiting them. In contrast to TFT, Pavlov loses against ALLD, because it alternates between C and D. By changing the decision rule slightly (e.g. 0.999, 0.001, 0.001, 0.995), however, this Pavlov-like strategy is evolutionarily stable against ALLD.