Generous TFT
According to Nowak and Sigmund (1992, 1993a, b) this weakness is caused
by the deterministic nature of the strategies discussed so far. In reducing
the probability for C or D specified by the outcome of the previous round
from 1 to <1, one takes random errors into account. For the infinitely
IPD (the limit case, w=1) the first move is irrelevant since
its effect is 'forgotten' in the long run (Nowak and Sigmund 1992). The
decision rule then consists of a point (p, q) in the unit square, with
the probability p (q) for a C after a cooperative (defective) move of the
partner; 0<p,q<1. In this terminology TFT corresponds to (1,0), ALLD
to (0,0), ALLC to (1, 1) and so on. In such a scenario, Generous tit for
tat (GTFT), a more forgiving strategy with q=min[l -(T-R)/(R-S), (R-P)/(T-P)]=
1/3 is said to provide the highest payoff (Nowak and Sigmund 1992).
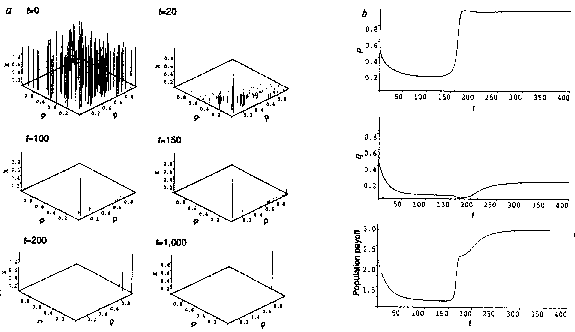
Fig. 3. The evolution of a set of strategies is shown.
99 strategies were randomly sampled and a TFT-like (0.99, 0.01) strategy
was added. The initial frequencies f were uniformly set to 0.01 and all
subsequent frequencies evolved in proportion to the payoff of the previous
round. a) Relative frequencies after 0, 20, 100, 150, 200, 1000 generations.
Strategies with very low frequencies may disappear from this plot, although
they are present in the numerical computations. b) Population averages
for p, q and payoff. See text for details. From: Nowak, M. A. and Sigmund,
K. 1992. Tit for tat in heterogeneous populations. Nature 355: 251.
Nowak and Sigmund (1992) used a similar approach as Axelrod in his ecological
tournament: 100 strategies S1 to S100 (uniformly
distributed on the unit square, equal initial relative frequencies) were
sampled, frequencies were assessed according to the payoff of the previous
round, below-threshold strategies were discarded and the frequencies evolved
as Fig. 3 shows: initially, the strategies closest to ALLD (0,0) feed on
a large percentage of high q suckers, and increase drastically while the
others vanish. If some of the initial strategies are close to TFT (1, 0),
however, the strategies near ALLD will never reach fixation: the depletion
of suckers reduces the exploiters' fitness (they now gain mostly P) while
the TFT-like strategies still obtain R interacting among themselves and
P confronting the defecting strategies. Slowly at first but gathering momentum,
the cooperators increase in frequency and the defectors wane. Yet, having
extinguished the ALLDlike strategies, the rules close to TFT are superseded
by a third strategy, very close to the less severe retaliator GTFT. Due
to the noise, generated by the stochasticity of the decision rules, the
harsh retaliation of TFT proved 'fatal' to TFT. The possibility of forgiveness
invading a retaliatorily cooperating community has previously been shown
(Boyd and Lorberbaum 1987); however, the simulations conducted by Nowak
and Sigmund (1992) clearly demonstrate the 'catalyser'-effect of TFT:
"TFT's strictness is salutary for the community,
but harms its own. [...] It needs to be present, initially only in a tiny
amount; in the intermediate phase, its concentration is high; but in the
end, only a trace remains."
|