Tit for tat
Axelrod and Hamilton (1981) used a computer tournament to detect strategies
that would favour cooperation among individuals engaged in the IPD. In
a first round, 14 more or less sophisticated strategies and one totally
random strategy competed against each other for the highest average scores
in an IPD of 200 moves. Unexpectedly, a very simple strategy did outstandingly
well: cooperate on the first move and then copy your opponent's last move
for all subsequent moves. This strategy was called 'Tit for tat' (TFT)
and became the founder of an ever growing amount of successful strategies.
In a similar competition with 62 contestants, TFT won again. It has three
characteristics that account for its impressive performance: it is nice
(cooperates on the first move), retaliatory (punishes defection in the
prior move with defection) and forgiving (immediate return to cooperation
after one C of the adversary).
In an ecological analysis, the scores from round two were used to calculate
the relative frequencies of the strategies in a hypothetical population.
The strategies were then submitted to each subsequent round in proportion
to their cumulative payoff (V) in the previous round. In
the long run, TFT outcompeted its rivals and went to fixation (Axelrod
and Hamilton 1981). Moreover, for
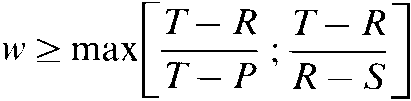 (2) (2)
where max denotes the larger of the two values in brackets, TFT can
increase in frequency in a predominantly ALLD environment and, once established,
resists invasion of any defecting strategy. Under these circumstances,
no single mutant can do better than TFT (TFT is "robust", Axelrod
and Hamilton 1981). Notwithstanding, there may be "twin"-strategies,
that do as well as TFT against TFTers. Any other cooperating strategy (e.g.
"always cooperate", ALLC) can perform a 'random walk' through
a homogenous TFT-population as they both get the same reward R. The relative
fitness of both strategies is equal, thus the selection coefficient s=0.
|