Hamilton’s Theory
Preliminary draft for the Encyclopedia of Genetics (Academic Press)
Get a pre-print in PDF or go to the Encyclopedia website!
A special tribute to W.D. Hamilton
Björn Brembs, Ph.D.
Selfish genes and cooperation
Paradoxically enough, inheritance is the basis of evolutionary change. Without safe transmission of genetic information from one generation into the next, there would be random arrangement of the genetic building blocks. Constant randomization of information carriers can obviously not lead to meaningful information. Thus, the cornerstone of evolution is genetics. Only after conserving well-tried genes can there be competition (selection) between new, yet untested ones (i.e. mutations). Charles Darwin (1809-1882) was the first to formulate a theory of gradual evolutionary change caused by adaptive mutations that are selected out of a number of other random variants. In a relentless “struggle for existence” many slightly different variants are competing with each other and only few survive. Darwin’s notion of “survival of the fittest” seems to convey the picture of a war in which everyone fights everyone. Nature is "red in tooth and claw", a merciless killing in which only the strongest and meanest can prevail. Victory (i.e. evolutionary success or ‘fitness’) is granted according to the reproductive success of the survivor. Again, only if the trait that led to successful reproduction is safely transmitted to the offspring, will this trait spread and eventually be represented as a feature of the species. Of course, if the trait in addition leads to procreation at a competitor’s expense, the animal not only gains fitness itself, but also reduces the fitness of those animals it is exploiting, increasing its odds even further. It is no wonder that parasitism and exploitation are widespread phenomena and virtually universal across the living world. Darwin himself emphasized: “No instinct has been produced for the exclusive good of other animals, but each animal takes advantage of the instincts of others”. Indeed this is one of the few truly falsifiable test statements in the Darwinian theory. And it seems so easily falsifiable: is there not ample evidence of cooperation in the animal kingdom? Parental care, shoaling fish, cooperatively hunting wolfs or lions, the mycchoriza symbiosis between the fungus and the plant, the subterranean colonies of the naked mole rat, coalition forming in primates or the social insects are but some of the most well known examples. Darwin was well aware of the problem and described it as "one special difficulty, which at first appeared to me insuperable, and actually fatal to the whole theory."
Group selection
In particular, Darwin was referring to the social insects. Already in those times it was common knowledge that hymenopteran colonies (honeybees, wasps, bumble bees and ants) usually consist of one reproducing queen and a multitude of sterile workers. This particular case of sociality is termed ‘eusociality’. In addition to sterile individuals cooperatively helping the fertile animals raising the offspring, eusociality is characterized by another trait: at least two generations overlap in life stages capable of contributing to colony labor, so that the offspring can assist their parents during part of their life cycle.
The abandonment of reproduction by the worker caste was the huge dilemma to which Darwin devoted an entire chapter in his ‘Origin of Species’. While the omnipresence of exploitation is well in accord with the rule ‘reproduce at the cost of your competitors’ the equally obvious existence of all degrees of altruism up to the complete sacrifice of reproductive success in favor of another organism seemed an insurmountable obstacle. How can individuals without own offspring exist if reproduction and inheritance are the foundation of the whole theory?
Darwin’s own solution was to assume that the colonies formed some sort of super-organisms that compete against each other in a very similar way as individuals do. To perceive animal colonies as super-organisms with their members as rough analogues of cells is a long known and, even today for certain studies, a very useful concept. The idea of family or “group selection” placated Darwin’s contemporaries and was still widely accepted well into the 20th century. According to this idea, the unit of selection for altruistic alleles of an originally selfish gene would be the colony or deme, not the individual. The altruistic, cooperative allele spreads in the species as colonies without a high occurrence (gene frequency) of this allele become extinct. However, in order for interdemic selection to be effective, one has to assume that there is no migration between the groups and that there is sufficient selection pressure, i.e. the rate of colony extinction is very high. Furthermore, individual selection will always be faster than group selection, as the number of individual organisms is much larger than that of populations and the turnover-rate of individuals is much higher. Thus, group selection can never counteract individual selection. Because of these considerations, group selection was eventually abandoned as the prime explanation for the evolution of cooperation. In its stead, William Donald Hamilton’s (1936-2000) discovered the principle of ‘kin selection’. Hamilton’s theory was published in the Journal of Theoretical Biology in 1964. At the time, it was so innovative that it almost failed to be published and was largely ignored for a decade. When finally noticed, its influence spread exponentially until it became one of the most cited papers in all of biology. It is the key to understanding the evolution of altruistic cooperation among related organisms, such as the social insects. Cooperation among unrelated individuals is beyond the scope of this article and is treated elsewhere (see bibliography and chapter ‘Prisoner’s Dilemma’).
Kin Selection
Why should there be a distinction between cooperation among unrelated individuals and that among related individuals at all? We have learned that genetics is the basis upon which evolutionary change is taking place. Fitness was defined above in terms of successful reproduction, i.e. the number of offspring carrying the selected allele. The more offspring, the “fitter” the parent. Darwin’s “struggle for existence” is a struggle for reproduction. With sexual reproduction, however, only one half of an organism’s genome is transferred into one of his offspring at a time. Therefore, any particular trait - depending on its mode of inheritance – is often transmitted from a parent to its offspring with a probability smaller than one. Thus, in order to transmit as many of one’s genes into the next generation as possible (and hence be evolutionarily successful), an organism has to produce as many surviving offspring as possible in order to maximize the probability of transmitting all its genetic information. This might constitute a difficult task, however, since all its competitors try to do the same. But there are other sources of one’s own genes available: relatives.
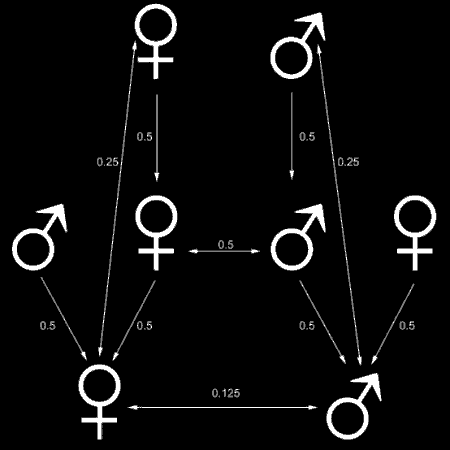
Fig. 1: The coefficient of relatedness. In diploid organisms, every parent (top row) transmits 50% of its genetic information to each offspring (middle row). On the average, siblings therefore share half of each parent’s contribution to their genome, adding to a coefficient of relatedness r=0.5. Consequently, cousins share an r=0.125 or r=1/8 (bottom row). Likewise, these cousins are related to their common grandparents by ¼ or r=0.25. One may also say that r is a measure for the probability that any given allele is shared by two individuals.
An ordinary diploid, sexually produced organism shares 50% of its genes with either of his parents. Accordingly, it shares about 50% with its siblings, 25% with its uncles, aunts, grandparents, grandchildren and so forth (coefficient of relatedness, see Fig. 1). Hamilton’s strike of genius was to reformulate the definition of fitness as the number of an individual’s alleles in the next generation. Or, more precisely, inclusive fitness is defined as an individual’s relative genetic representation in the gene pool in the next generation:
![]() (1)
(1)
Thus, fitness denotes the capability of an allele to spread in a population: if the fitness value for a given allele is larger than one it will increase in frequency and if it is smaller it will decrease in frequency. It is evident that such ‘genic (as opposed to group) selection’ will favor an allele that not only enhances reproductive success of its carrier but also of all other individuals sufficiently related to it. But could an allele that reduces its carriers fitness while enhancing its relatives’ fitness be adaptive? Would it spread in a natural population? This is not a trivial question and it takes some computational effort to solve it. Let’s try to formulate the inclusive fitness w of an individual i. As noted in equation (1), w should be composed of the fitness a of the focal individual and the contribution x of its relatives:
wi = ai + x (2)
The contribution x to individual i’s inclusive fitness w is then the sum of all alleles in the gene pool that are shared by i and it’s relatives j:
![]() (3)
(3)
where r is the coefficient of relatedness between individual i and its relative j, and b is the fitness of j. Note that always r >= 1 and therefore j’s contribution to wi depends critically on its relatedness to i. We can thus reformulate equation (2) to
![]() (4)
(4)
Obviously, if the allele in question infers a fitness cost (i.e. ai < 1), wi will only be greater than one if r is sufficiently high (given that the higher fitness b of the relative also means higher cost). Reformulating equation (4) into a cost (C) / benefit (B) relation describing the necessity of wi being greater than one if the allele of interest is to spread, yields
1 – C + rB > 1 (5)
which can be easily rearranged to produce Hamilton’s rule:
![]() (6)
(6)
Put into words, the relatedness of the individual that profits from the altruistic act of the focal individual must be higher than the cost/benefit ratio this act imposes. Thus the question whether ‘cooperative’ genes may spread even if the cooperation infers fitness costs, can be solved both by simulation to find out the critical ranges of the parameters in question and experimentally by measuring the relevant parameters and comparing them to the simulated results.
A very simple example will explain the concept. Consider a pair of brothers (r = 0.5, see Fig. 1) from which one sacrifices all of his fitness (C = 1) due to not reproducing but helping his brother to successfully rear offspring. In order for C/B to become smaller than r = 0.5, the altruist’s act must at least double the receiver’s fitness in order for the altruist to gain representation in the next generation. Evidently, a very high coefficient of relatedness is needed to overcome high fitness costs due to sterility or decrease in life expectancy or both. The benefit of altruism decreases rapidly with declining relatedness. It becomes clear that the distinction between cooperation among related and among unrelated individuals is vital for understanding the evolution of cooperation.
Hamilton’s rule and the social insects
Why did Hamilton’s theory have such an impact on modern evolutionary biology? Of course, most of all because it provided the possibility to explain the evolution of a significant part of all the cooperation occurring in nature without having to resort to group selection and its very restrictive assumptions. But there is another piece of evidence that furnishes a beautiful theory with a cream topping: the haplo-diploid sex determination of the social hymenopterans, i.e. the bees, ants and wasps – the very insects that posed such a severe puzzle to Darwin.
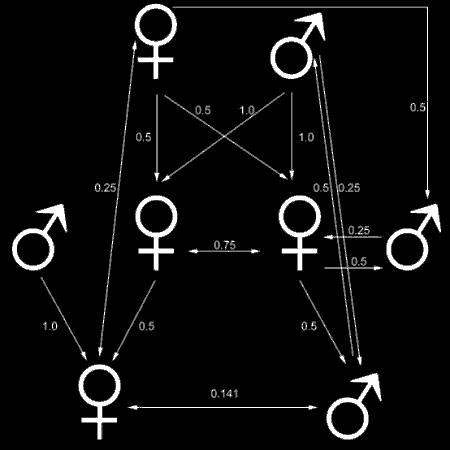
Fig. 2: The coefficient of relatedness with haplodiploid sex determination. Note how the coefficients are skewed with respect to the diploid system depicted in Fig. 1. For example, sisters (middle row) are more related to each other (r=0.75) than they are to their mother (top row; r=0.5).
While most animal genera have a hetero- and a homogametic sex (i.e. a different set of sex chromosomes for the different sexes), hymenopterans universally produce males from unfertilized (i.e. haploid) eggs and females from fertilized (i.e. diploid) eggs. This system skews relatedness in an almost perfect way for eusociality to evolve (see Fig. 2). Consider a female worker. Half of its genome comes from the father (haploid) and half from the mother (diploid). That means she carries all of her fathers genes and half of her mother’s genes. So does her sister, implying that they share of course the entire genome of their common father (i.e. already 50% of their genome), plus, on average, a quarter of their mother’s genome, yielding a coefficient of relatedness of 0.75. Thus altruistically helping their mother (the queen) and her offspring (new founding queens and workers) needs only to yield a small benefit (compared to "normal" diploid organism) in order to spread through the population.
Accordingly, the hymenopterans are the order with the highest occurrence of eusociality in the animal kingdom: eusociality has arisen at least eleven times independently during the evolution of the hymenopterans. Only a few species within the Arthropoda are known to be eusocial such as the termites (Isoptera) and some aphids (Hemiptera). Outside the Arthropoda, the only species known to form eusocial colonies is the naked mole rat (Heterocephalus glaber). This prevalence of eusociality within the hymenopterans is very suggestive of Hamilton’s rule having a deep impact on their evolutionary path.(Note that haplo-diploidy is not sufficient, however, to create sociality because most hymenopteran species are solitaire.) In the light of kin selection, even Darwin’s notion of family or group selection can be seen in a different light: now the otherwise weak interdemic selection can act additively together with genic selection also against individual selection to spread cooperative genes in a population.
Bibliography:
Brembs, B (1996) “Chaos cheating and cooperation: potential solutions to the Prisoner's Dilemma” Oikos 76: 14-24.Futuyma, D.J. (1986) “Evolutionary Biology” Sinauer Associates, Inc.; ISBN: 0878931880
Hamilton, W.D.. (1996) "Narrow Roads of Gene Land" Oxford University Press; ISBN: 0716745305
Hölldobler, B. and Wilson, E.O. (1990) "The Ants" Belknap Press; ISBN: 0674040759