Ambulatory organisms are faced with the task of surviving in a rapidly changing environment. As a consequence, they have acquired the ability to learn. Most learning situations comprise one or more initially neutral stimuli (conditioned stimulus, CS), the animal’s behavior (B) and a biologically significant stimulus (unconditioned stimulus, US). Freely moving animals experience a stream of perceptions that is crucially dependent on the animal’s behavior. Opening or closing the eyes, directing gaze or ears, sniffing, biting or locomotion all have sometimes drastic effects on the animal’s stimulus situation. The archetypal example of such a learning situation is a frog or toad trying to eat a bee or wasp. During the search for prey (B₁), movement detectors in the anuran’s eye detect the hymenopteran’s locomotion (S₁). The frog will perform a taxis or approach towards the prey (B₂). There is no apparent difference in the frog’s behavior whether the prey is colored brightly (CS) or dull, if the frog is naive, i.e. has not encountered bees before. If the bee continues to move and fits some other criteria to classify it as appropriate prey (S_n), the frog will try to catch it using his extendable, adhesive glossa (B₃). The sting of the bee (US) will lead to immediate rejection (B₄). One can describe this sequence more generally as B₁ leading to S₁ which causes B₂ which in turn is followed by the perception of the CS. The S₁ does not only causes B₂, but in conjunction with other stimuli (S₁+S_n) leads to B₃ which makes the bee sting (US) which in turn leads to B₄. In other words, close temporal proximity can often be regarded as a clue for a causal relationship. This is a central insight for the understanding of associative learning. It becomes clear that stimuli can be both causes and consequences of behaviors.

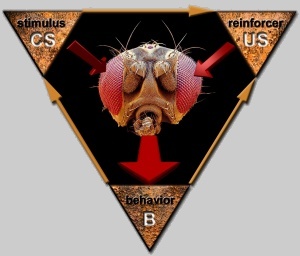Fig. 1: Drosophila in a natural learning situation. The animal’s CNS spontaneously generates motor patterns which manifest themselves in behavior (B). B either alters some of the stimuli currently exciting the sensory organs of the fly or leads to the perception of new stimuli. If one of these stimuli has a direct feedback onto the behavior, i.e. the perception of the stimulus persistently leads to the production of a particular behavior, this stimulus can be a reinforcer (US). If a certain behavior consistently leads to perception of the reinforcer, the animal can learn about this relationship in order to avoid aversive or obtain appettitive reinforcers (i.e. form a B-US association). Sometimes the US is consistently accompanied by an initially neutral stimulus (CS). In these cases, there is the possibility to learn about the relation between the CS and the US (i.e. form a CS-US association) in order to anticipate the appearance of the US. As CS and US share a temporal relationship and both are controlled by the B, in such a situation both B-US, B-CS and CS-US associations can form. Red arrows – neuro-physical or physico-neural interactions, brown arrows – physico-physical interactions. (Scanning electron micrograph courtesy of ‘Eye of Science’)

Therefore, the ‘three term contingency’ (Skinner, 1938) between B, CS and US is best described using feedback loops. The animal’s brain chooses an action (B) from its behavioral repertoire which will have consequences on the animal’s stimulus situation (CS, US), which will in turn enter the brain via sensory organs and influence the next choice of B (Fig. 1). Eventually, the frog will continue to forage (B₁) after some time and the whole sequence can start anew. It is common knowledge that if the prey exhibits the CS at a subsequent encounter, at least B₃ will not occur. Often a behavior similar to B₄ can be observed and sometimes B₂ will also be left out.  

Evidently, on occasions like the one described above the animal learns that the CS is followed by an aversive US. Such learning about relations between stimuli is referred to as Pavlovian or classical conditioning. Classical conditioning is often described as the transfer of the response-eliciting property of a biologically significant stimulus (US) to a new stimulus (CS) without that property (Pavlov, 1927; Hawkins et al., 1983; Kandel et al., 1983; Carew and Sahley, 1986; Hammer, 1993). This transfer is thought to occur only if the CS can serve as a predictor for the US (Rescorla and Wagner, 1972; Pearce, 1987; Sutton and Barto, 1990; Pearce, 1994). Thus, classical conditioning can be understood as learning about the temporal (or causal; Denniston et al., 1996) relationships between external stimuli to allow for appropriate preparatory behavior before biologically significant events ("signalization"; Pavlov, 1927). Much progress has been made in elucidating the neuronal and molecular events that take place during acquisition and consolidation of the memory trace in classical conditioning (Kandel et al., 1983; Tully et al., 1990; Tully, 1991; Tully et al., 1994; Glanzman, 1995; Menzel and Müller, 1996; Fanselow, 1998; Kim et al., 1998).
On the other hand, the animal has learned that its behavior B3 caused (was followed by) the US and therefore suppresses it in subsequent encounters. Such learning about the consequences of one's own behavior is called instrumental or operant conditioning. In contrast to classical conditioning, the processes underlying operant conditioning may be diverse and are still poorly understood. Technically speaking, the feedback loop between the animal's behavior and the reinforcer (US) is closed. Obviously, a behavior is produced either in response to a stimulus or to obtain a certain stimulus situation (goal) or both. Thus, operant conditioning is characterized mainly by B-US but also by B-CS associations (see for a general model: Wolf and Heisenberg, 1991). Analysis of operant conditioning on a neuronal and molecular level is in progress (Horridge, 1962; Hoyle, 1979; Nargeot et al., 1997; Wolpaw, 1997; Spencer et al., 1999; Nargeot et al., 1999a; b) but still far from a stage comparable to that in classical conditioning.
Considering the example above, it becomes clear that more often than not operant and classical conditioning can not be separated as clearly as they are separated in the literature. As the appropriate timing is the key criterion for both types of learning to occur, both operant and classical conditioning can be conceptualized as detection, evaluation and storage of temporal relationships. One recurrent concern in learning and memory research, therefore, has been the question whether for operant and classical conditioning a common formalism can be derived or whether they constitute two basically different processes (Gormezano and Tait, 1976). Both one- (Guthrie, 1952; Hebb, 1956; Sheffield, 1965) and two-process theories (Skinner, 1935; Skinner, 1937; Konorski and Miller, 1937a, b; Rescorla and Solomon, 1967; Trapold and Overmier, 1972) have been proposed from early on, and still today the issue remains unsolved, despite further insights and approaches (Trapold and Winokur, 1967; Trapold et al., 1968; Hellige and Grant, 1974; Gormezano and Tait, 1976; Donahoe et al., 1993; Hoffmann, 1993; Balleine, 1994; Rescorla, 1994; Donahoe, 1997; Donahoe et al., 1997).
As exemplified above, often it is impossible to discern the associations the animal has produced when it shows the conditioned behavior. In a recent study, Rescorla (1994) notes: "...one is unlikely to achieve a stimulus that bears a purely Pavlovian or purely instrumental relation to an outcome". With Drosophila at the torque meter (Heisenberg and Wolf, 1984; Heisenberg and Wolf, 1988), this disentanglement of Skinner's now classic three term contingency has been achieved. Classical and operant learning can be separated with the necessary experimental rigor and directly compared in very similar stimulus situations to show how they are related.

2.2.1 Drosophila at the torque meter

In visual learning of Drosophila at the torque meter (Fig. 2; Wolf and Heisenberg, 1991; Wolf and Heisenberg, 1997; Wolf et al., 1998; Liu et al., 1999) the fly's yaw torque is the only motor output recorded. The fly is surrounded by a cylindrical arena that may be used for stimulus presentation. Most simply, yaw torque can be made directly contingent on reinforcement (infrared light delivering instantaneous heat) with none of the external stimuli bearing any relation to the reinforcer (yaw torque learning; Wolf and Heisenberg, 1991; Fig. 3I). The fly learns to switch the reinforcer on and off by producing yaw torque of a certain range without the aid of additional stimuli. Adding a CS (color or patterns) to this set-up brings about a new operant paradigm at the torque meter to be called switch (sw)-mode (Fig. 3II). The color of the arena illumination (or the orientation of patterns on the arena) is exchanged whenever the yaw torque of the fly changes from the punished to the unpunished range and vice versa. 

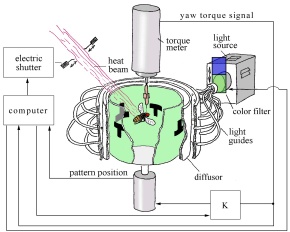Fig. 2: Flight simulator set-up. The fly is flying stationarily in a cylindrical arena homogeneously illuminated from behind. The fly’s tendency to perform left or right turns (yaw torque) is measured continuously and fed into the computer. The computer controls pattern position (via the motor control unit K), shutter closure and color of illumination according to the conditioning rules.

   More sophisticatedly, the angular speed of the arena can be made negatively proportional to the fly's yaw torque, enabling it to stabilize the arena, i.e. to fly straight (closed loop; Wolf and Heisenberg, 1991; for detailed explanation see MATERIALS AND METHODS). In this flight simulator (fs)-mode (Fig. 3III), the fly can learn to avoid flight directions denoted by different patterns (operant pattern learning) or by different arena coloration (operant color learning; Wolf and Heisenberg, 1997). In the latter case, a uniformly patterned arena is used to allow for turn integration to occur. Using both colors and patterns as visual cues in fs-mode results in operant compound conditioning.
Finally, the fly's behavior may have no relation whatsoever with the appearance of the heat, but the reinforcer is contingent upon the presentation of a CS. Wolf et al. (1998) have first described classical pattern learning at the flight simulator (Fig. 3IV). The setup is identical to the operant pattern learning paradigm, except for the training phase where the fly cannot interfere with pattern presentation (open loop). Again, this setup can also be used with identical patterns and different arena illumination (classical color learning). In all instances learning success (memory) is assessed by recording the fly's behavior once the training is over.
Thus, all components of the three term contingency are available: the behavior B (yaw torque), the reinforcer or US (heat) and a set of conditioned stimuli or CSs (colors or patterns). The flexible setup enables the establishment of virtually all possible combinations between the three components for later fine dissection of the associations the fly has formed during the training phase.

2.2.2 Initial framework and assumptions

The components of the three term contingency B, CS and US can be arranged in at least the four different ways depicted in Fig. 3. The four situations can be grouped into single-association or monodimensional tasks (Fig. 3 I + IV) and composite or multidimensional tasks (Fig. 3 II + III). The monodimensional tasks require only simple CS-US or B-US associations in order for the animal to show the conditioned behavior. The multidimensional tasks are more complex and offer the possibility of forming a number of different associations, each of which may be sufficient to show the appropriate learning. Usually it is not clear, which of the associations are formed. Composite learning situations are always operant tasks as the feedback loop between the stimuli and the behavior is closed. They are of two types: (1) Situations in which the CS is only paralleling the appearance of the US, i.e. the change in a behavioral program primarily determines reinforcer presentation (B-US). In the sw-mode the CS parallels the appearance of the US during a 'pure' operant conditioning process and the CS-US association forms in parallel to the concomitant motor program modulation. The fly learns to avoid the heat by restricting its yaw torque range and at the same time the heat can induce the pattern or color preference (CS-US association). One can thus refer to situations like this as 'parallel'-operant conditioning. Parallel-operant conditioning in essence is the additive combination of classical and pure-operant conditioning. (2) Situations in which the behavior controls the CS onto which the US is made contingent; i.e. there is no a priori contingency between a motor program and the reinforcer as in (1). Direct B-US associations can not occur, but the behavioral control of the CS may induce (maybe US mediated) B-CS associations. This type of situations may be called 'operant stimulus conditioning'. All types of learning have in common that either a behavior (Fig. 3 I) or a stimulus (Fig. 3IV) or both (Fig. 3 II, III) can in principle be used as predictors of reinforcement. From this formal point of view, behaviors and predictors can be treated as equivalent entities as long as the experimental design ensures equal predictive value. In other words, provided that both behaviors and stimuli in a composite conditioning experiment can be used equally well to predict reinforcement, both B-US and CS-US associations should be formed. Similarly, if the formal description holds, the single-association tasks (Fig. 3 I + IV) should not differ, i.e. they should require similar amount of training.

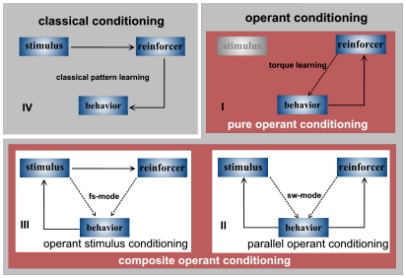
Fig. 3: Block diagram of the experiments used in this study. Solid arrows – feedforward relations; dotted arrows – feedback relations. Note that only the logical relationship between the components of the learning situation is depicted. Neither the way the experiment works, nor the possible associations nor any physical relationships are addressed.

2.2.3 Analyzing the components in Drosophila learning

Since operant pattern learning at the torque meter was first reported (Wolf and Heisenberg, 1991), the method has been used to investigate pattern recognition (Dill et al., 1993; Dill and Heisenberg, 1995; Dill et al., 1995; Ernst and Heisenberg, 1999) and structure function relationships in the brain (Weidtmann, 1993; Wolf et al., 1998; Liu et al., 1999). Dill et al. (1995) have started a behavioral analysis of the learning/memory process and others (Eyding, 1993; Guo et al., 1996; Guo and Götz, 1997; Wolf and Heisenberg, 1997; Xia et al., 1997a, b; Wang et al., 1998; Xia et al., 1999) have continued. Yet, a formal description of how the operant behavior is involved in the learning task is still in demand.
In contrast to operant pattern learning, the formal description for classical pattern learning seems rather straightforward: In order to show the appropriate avoidance in a subsequent closed-loop test without heat the fly has to transfer during training the avoidance-eliciting properties of the heat (US+) to the punished pattern orientation (CS+), and/or the 'safety'-signaling property of the ambient temperature (US-) to the alternative pattern orientation (CS-). As the fly receives no confirmation which behavior would save it from the heat, it is not able to associate a particularly successful behavior with the reinforcement schedule. In other words, it is assumed that classical conditioning is solely based on an association between CS and US and not on any kind of motor learning or learning of a behavioral strategy. 
As both operant and classical pattern training lead to an associatively conditioned differential pattern preference, it is clear that also during operant training a CS-US association must form. Knowing that this association can be formed independently of behavioral modifications, one is inclined to interpret the operant procedure as classical conditioning taking place during an operant behavior (pseudo-operant). However, Wolf and Heisenberg (1991) have shown that operant pattern learning at the flight simulator is not entirely reducible to classical conditioning. In a yoked control in which the precise sequence of pattern movements and heating episodes produced by one fly during operant (closed loop) training was presented to a second fly as classical (open loop) training, no learning was observed. 
Two interesting questions arise from these findings: (1) Why does this form of training not show a learning effect despite the fact that flies in principle are able to learn the patterns classically (Wolf et al., 1998)? Why do Wolf et al., (1998) find classical pattern learning but Wolf and Heisenberg (1991) do not? A more extensive yoked control is performed to find an answer to this question. (2) Why does the same stimulus sequence lead to an associative aftereffect if the sequence is generated by the fly itself (operant training), but not if it is generated by a different fly (classical replay training, yoked control)? What makes the operant training more effective? Two possible answers have been addressed. For one, the operant and the classical component might form an additive process. In other words, during operant conditioning the fly might learn a strategy such as: "Stop turning when you come out of the heat" in addition to the pattern-heat association. The operantly improved avoidance behavior would then amplify the effect of the CS-US association upon recall in the memory test. This question was tackled by Brembs (1996) and is thoroughly discussed and rejected there. As the alternative, the coincidence of the sensory events with the fly's own behavioral activity (operant behavior) may facilitate acquisition of the CS-US association. In this case, there would be no operant component stored in the memory trace (only operant behavior during acquisition) and thus the classical CS-US association would be qualitatively the same as in classical conditioning. A transfer of this CS-US association learned in one behavior to a new behavior would be compatible with such an hypothesis.
The approach just described compares a simple classical with a composite operant conditioning procedure in which both classical and operant components may occur, in order to find out more about the contribution of the operant (B-US, B-CS) component to pattern learning in Drosophila. In a second set of experiments a single association operant task (yaw torque learning, only B-US associations required) to compare with a second composite operant task (sw-mode) with both operant and classical components, in order to learn more about the classical (CS-US) contribution. The formal description of yaw torque learning is rather straightforward: once the fly has successfully compared the temporal structure of the heat with its motor output, it has to transfer the avoidance eliciting properties of the heat to the punished range of its yaw torque generating motor programs (i.e. it has to form a B-US association). In the subsequent test phase, these motor programs have to be suppressed (avoided) in favor of other programs in order to show a learning score. With classical pattern learning and yaw torque learning being 'pure' experiments where single associations are assumed to be formed, both fs-mode and sw-mode conditioning are composite forms of learning where the formation of two or more associations are possible. Assessment of the contribution of both classical and operant components to sw-mode learning is brought about by rearranging or separating behavior and stimulus.
With this array of experiments, it should be possible to estimate the contribution of behavioral and sensory predictors to complex, natural learning situations. The hypothesis to be tested, derived from the formal considerations above, is the equivalence of B-US and CS-US associations: are both operant and classical associations formed?
Once the relations and interactions of the individual associations during memory acquisition within a complex learning task are elucidated, the next logical step is to analyze the single associations more closely. It was mentioned above that behavior is not produced for its own sake, but rather to achieve a certain stimulus situation or goal ('desired state'; Wolf and Heisenberg, 1991). Moreover, some behaviors occur more frequently upon perception of a given stimulus than other behaviors, i.e. certain stimuli have (or have acquired) the potential to elicit certain behaviors. Thus, stimulus processing is of outstanding importance for the understanding of learning and memory. Therefore, the acquisition of stimulus memory is subjected to closer scrutiny. Here, the Drosophila flight simulator offers a unique opportunity for studying the properties of the CS-US association (i.e. the associations formed if more than one CS-US association is allowed). First, there are, to my knowledge, no studies explicitly dealing with compound stimulus learning in a complex situation. As mentioned above, most experiments do comprise both operant and classical components regardless of the initial intent to separate them. However much the operant and classical components may vary, though, the degree to which the behavior controls the animal's stimulus situation in unsurpassed in the flight simulator. Second, the flight simulator in its restrictedness offers the experimenter exquisite control over the stimuli the animal perceives and thereby minimizes the amount of variation between animals. Most confounding variables that complicate other learning experiments are eliminated in the flight simulator. Third, the recent development of operant compound conditioning in the flight simulator enables the experimenter to investigate into complex processes hitherto mainly studied in vertebrates.

There can be no doubt that stimulus learning is not only of prevalent importance for the animal's survival, but the literature on associative learning is strongly biased towards this type of association as well. The vertebrate literature is dominated by both operant and classical experiments in a number of species dealing with the properties of the CS-US acquisition process. The results reveal a surprising generality across the varying degree of operant and classical influences as well as across species. This generality has led to the development of quantitative rules characterizing associative stimulus learning and hence the suggestion of common learning mechanisms across phyla (Pavlov, 1927; Skinner, 1938) and across traditionally distinct paradigms as classical and operant conditioning (Skinner, 1938; Trapold and Winokur, 1967; Trapold et al., 1968; Grant et al., 1969; Mellgren and Ost, 1969; Feldman, 1971; Hellige and Grant, 1974; Feldman, 1975; Williams, 1975; McHose and Moore, 1976; Pearce and Hall, 1978; Williams, 1978; Zanich and Fowler, 1978; Williams and Heyneman, 1982; Ross and LoLordo, 1987; Hammerl, 1993; Rescorla, 1994; Williams, 1994; Lattal and Nakajima, 1998). It would be interesting to know how far this generality can be stretched.

How can one formally conceptualize the acquisition of memory? Usually, the simple notion of pairing CS and US is formalized as the amount or increment of learning (DV) being proportional to the product of reinforcement (l) and the associability (a) of the CS (e.g. Rescorla and Wagner, 1972; Pearce and Hall, 1980).

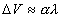(1)

More typically, inequality (1) is refined as DV being proportional to the difference between the actual level of reinforcement (l) and the amount of learning already acquired (i.e. the degree to which the US is signaled or predicted by the CS: 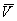). Modifying the reinforcement term yields an asymptotic learning rule – the so-called ‘delta rule’:

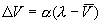, (2)

This class of learning theories has also been called "error correcting learning rules" because increments in learning lead to 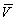 approaching l and thereby correct the error between observation and prediction. Several such rules refining and extending the simple concept that temporal pairing of CS and US are necessary and sufficient to form an association between them have been found in vertebrates (Rescorla and Wagner, 1972; Mackintosh, 1975b; Pearce and Hall, 1980; Sutton and Barto, 1981; Pearce, 1987; Sutton and Barto, 1990; Pearce, 1994). The most commonly observed phenomena providing evidence for such rules are 'overshadowing' (Pavlov, 1927), 'blocking' (Kamin, 1968), 'sensory preconditioning' (Brogden, 1939; Kimmel, 1977) and second-order conditioning (Pavlov, 1927).

Overshadowing may occur in a conditioning experiment when a compound stimulus, composed of two elements, is paired with the reinforcer (CS1+CS2+US). If the elements of the compound differ in associability, the conditioned response is stronger for the more associable stimulus than for the other. Thus one stimulus 'overshadows' the other (Pavlov, 1927). Overshadowing is a well known phenomenon from classical (Pavlov, 1927) and operant (Miles, 1969; Miles and Jenkins, 1973) conditioning in vertebrates and from invertebrates (Couvillon and Bitterman, 1980; Couvillon and Bitterman, 1989; Couvillon et al., 1996; Pelz, 1997; Smith, 1998). The degree to which different stimuli can overshadow each other depends largely on their modalities and is usually correlated with their physical intensity (Mackintosh, 1976). As will become clear below, overshadowing may interfere with blocking, sensory preconditioning and second-order conditioning experiments.
Blocking implies that temporal CS-US pairing does not transfer the response-eliciting property of the US to the CS if the CS is presented together with another CS that already fully predicts the US. In a classical blocking design, a first (pretraining) phase consists of training one stimulus (CS1+US) until the subject shows a maximal learning response. Subsequently, a new stimulus (CS2) is added and the compound is reinforced (CS1+CS2+US). If afterwards CS2 is tested alone, the subject shows a learning score below that of a control group that has not received any pretraining. Thus, the pretraining has 'blocked' learning about CS2 (Kamin, 1968). Part 2 of this procedure is very similar to an overshadowing experiment and hence it becomes clear that ideally the elements of the compound should not show overshadowing without any pretraining (but see Schindler and Weiss, 1985; Weiss and Panilio, 1999 for sophisticated two compound operant experiments with rats and pigeons, respectively, that can overcome strong overshadowing effects and produce blocking).
Often blocking is explained in terms of predictability or expectation: only if a US is 'surprising' (Kamin, 1968; Kamin, 1969), i.e. if it is not well predicted, can the stimuli having a predictive value for the US enter into the association. In a blocking experiment, the novel CS2 is compounded with the already well trained CS1 as a redundant predictor. Thus, CS2 accrues less associative strength than if no pretraining had occurred (Rescorla and Wagner, 1972; Pearce and Hall, 1980; Sutton and Barto, 1981; Sutton and Barto, 1990; Pearce, 1994). Blocking was initially developed in classical (Pavlovian) conditioning paradigms (e.g. Kamin, 1968; Fanselow, 1998; Thompson et al., 1998). It was later extended also to instrumental (operant) conditioning, using discriminative stimuli (SD; e.g. Feldman, 1971; Feldman, 1975) and is now widely generalized to operant conditioning together with other prominent concepts like 'unblocking' and 'overexpectation' (e.g. McHose and Moore, 1976; Haddad et al., 1981; Schindler and Weiss, 1985; Williams, 1994; Lattal and Nakajima, 1998; Weiss and Panilio, 1999). Operant SDs, however, only indicate during which time the B-US contingency is true and thus share a feature with 'classical' CSs: they are at most only partially controlled by the animal. While it seems that SDs are not entirely reducible to classical CSs (e.g. Holman and Mackintosh, 1981; Rescorla, 1994), they still are very different from the stimuli controlled entirely by the animal as in the flight simulator. I do not know of any study using this type of operant conditioning to produce blocking. It would be interesting to find out whether the high degree of operant control over the stimuli as in the flight simulator has any effect on blocking. 
Even though our understanding of the ecological significance (Dukas, 1999) and neural mechanisms underlying blocking is still in its infancy (Holland, 1997; Fanselow, 1998; Thompson et al., 1998), it has become a cornerstone of modern learning theories (Rescorla and Wagner, 1972; Pearce and Hall, 1980; Sutton and Barto, 1981; Wagner, 1981; Sutton and Barto, 1990; Pearce, 1994). The discovery of blocking by Kamin (1968), has had a large impact on research in many vertebrates (e.g. Marchant and Moore, 1973; Bakal et al., 1974; Mackintosh, 1975a; Cheatle and Rudy, 1978; Wagner et al., 1980; Schachtman et al., 1985; Barnet et al., 1993; Holland and Gallagher, 1993; Batsell, 1997; Thompson et al., 1998) including humans (e.g. Jones et al., 1990; Kimmel and Bevill, 1991; Levey and Martin, 1991; Martin and Levey, 1991; Kimmel and Bevill, 1996). The literature on invertebrates is more scarce. Reports include honeybees (Smith, 1996; Couvillon et al., 1997; Smith, 1997; Smith, 1998), Limax (Sahley et al., 1981) and Hermissenda (Rogers, 1995; Rogers et al., 1996). In all instances, however, confounding effects have been pointed out and remain to be solved (Farley et al., 1997; Gerber and Ullrich, 1999). To my knowledge, there is no unambiguous evidence in the literature that invertebrates exhibit blocking.
In second-order conditioning (SOC) a stimulus (CS1) is paired with a US until it has acquired a predictive function for the US. In the second part of the experiment the CS1 is paired with a CS2 but without reinforcement. Finally, the CS2 is presented alone to test whether by having been paired with the CS1 it has become a predictor of the US as well. One can perceive an SOC experiment as a blocking experiment where the reinforcement is omitted in the compound phase. However, in SOC a positive learning score indicates a successful experiment, whereas blocking would be indicated by a negative result (compared to control groups). Thus, SOC constitutes an important control of the blocking experiment: if blocking is not obtained, it might be due to SOC masking a potential blocking effect. As the analogy of a blocking experiment to SOC is striking, one can wonder how blocking can be observed at all. A pioneering study by Cheatle and Rudy (1978) suggests that reinforcement during compound training disrupts the transfer of the response eliciting properties from the pretrained CS1 to CS2. This is compatible with newer neurobiological data (Hammer, 1993; Hammer, 1997; Fanselow, 1998; Kim et al., 1998) that imply a negative feedback mechanism to attenuate US effectiveness if reinforcement is well predicted (Fanselow, 1998; Kim et al., 1998) and instead lead to a US representation upon perception of the CS (Hammer, 1993; Hammer, 1997). SOC has been found in both vertebrates (Rizley and Rescorla, 1972; Holland and Rescorla, 1975a; Holland and Rescorla, 1975b; Cheatle and Rudy, 1978; Rescorla, 1979; Rescorla and Cunningham, 1979; Amiro and Bitterman, 1980; Rescorla and Gillan, 1980; Rescorla, 1982; Hall and Suboski, 1995) and invertebrates (Takeda, 1961; Sekiguchi et al., 1994; Hawkins et al., 1998; Mosolff et al., 1998).
Sensory Preconditioning (SPC) is formally very similar to SOC. It again consists of three parts. In the first, the subject is presented with two stimuli (conditioned stimuli; CS1+CS2) without any reinforcement. Then, one of the stimuli (CS1) is reinforced alone. Provided the appropriate controls exclude alternative explanations, a significant learning score in the third phase testing the other stimulus (CS2) alone demonstrates that the response eliciting properties of the unconditioned stimulus (US) have been transferred to a CS with which it has never been paired. Compared to SOC the sequence of parts 1 and 2 is inverted. While thus SOC can be regarded as the temporally reversed analogue of SPC, there is one important difference between SPC and SOC: in vertebrates, extinction of the reinforced CS1 prior to testing of CS2 abolishes SPC but not SOC (e.g. Rizley and Rescorla, 1972; Cheatle and Rudy, 1978; Rescorla, 1983). Additional reported features of SPC comprise the dependence of the intensity of the non-reinforced but not of the reinforced CS (Tait and Suboski, 1972) and of the number of preconditioning trials (Prewitt, 1967; Tait et al., 1972), but see (Hall and Suboski, 1995 for zebrafish). Another especially noteworthy property of SPC is the less restrictive timing dependence in the CS1+CS2 compound phase: in rats, simultaneous pairings show stronger effects than sequential ones (Rescorla, 1980; Lyn and Capaldi, 1994) and backward pairing leads to excitatory, rather than inhibitory associations (Ward-Robinson and Hall, 1996; Ward-Robinson and Hall, 1998; see Hall, 1996 for a review). SPC may be perceived as a case of 'incidental learning' where CS1 becomes associated with CS2 (see DISCUSSION). There is one report on incidental learning at the flight simulator (novelty choice) by Dill and Heisenberg (1995). Flies can remember patterns without heat reinforcement and compare them to other patterns later.
Some of the above mentioned phenomena have warranted explanations that include cognition-like concepts of attention or expectation and prediction. The two types of CSs (visual patterns, colors) open the possibility to study the effects of compound CSs and, in particular, to investigate whether overshadowing, blocking, SOC and SPC can be observed in flies. It is interesting to find out whether these phenomena are implemented in the fly and hence learning rules developed in vertebrates also apply to Drosophila visual learning. Moreover, the recent discovery of context generalization in Drosophila at the flight simulator by Liu et al. (1999) have shown that associative stimulus learning is still little understood.